Les 3 points-clefs
OOrigines et Importance des Nombres Figurés
L’addition théosophique, utilisant des cailloux (calculi), est une méthode antique, revitalisée par l’École de Pythagore. Platon et ses disciples, comme Speusippe, ont écrit sur l'importance des nombres, associant Un au point, Deux à la ligne, Trois au plan et Quatre au volume. Les nombres figurés visualisent les concepts numériques dans l'espace, rendant la compréhension intuitive.
AAddition Théosophique et Nombres Triangulaires
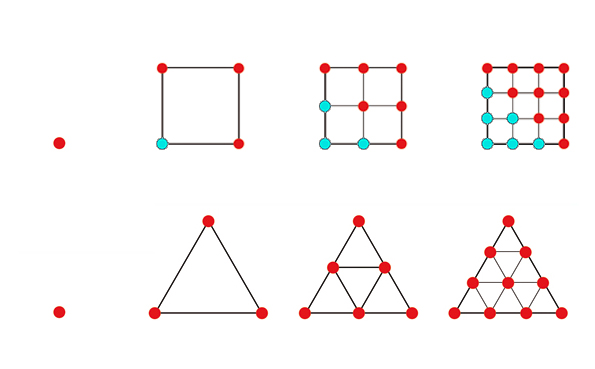
Pour effectuer l'addition théosophique d'un nombre, on additionne tous les chiffres de 1 jusqu'à ce nombre. Par exemple, pour le nombre 4 : 1 + 2 + 3 + 4 = 10. Cette méthode est liée aux nombres triangulaires, obtenus par l'addition séquentielle des nombres entiers : 1, 3, 6, 10, etc. Les nombres triangulaires sont une catégorie de nombres figurés formant des figures géométriques régulières.
CNombres Carrés et Combinatoire
Les nombres triangulaires sont essentiels dans la logique combinatoire, débutant par le dénombrement des relations entre deux éléments. Un nombre carré est la somme de deux nombres triangulaires consécutifs : 1 = 1, 4 = 1 + 3, 9 = 3 + 6, 16 = 6 + 10. Cette relation illustre comment les nombres et les formes géométriques interagissent pour révéler des structures mathématiques fondamentales.