- La langue des nombres
- Symboles des 9 nombres
- Systèmes symboliques numériques
- 1. Les 22 polygones du cercle
- 2. L'alchimie du Yi King
- 3. Le triangle de Pascal
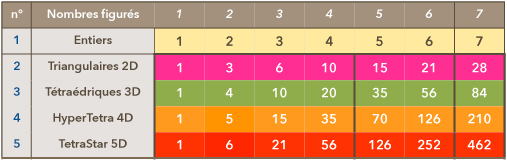
- 4. La Tetractys de Pythagoe
- 5. Les 5 solides de Platon
- 6. L'Âme du Monde du Platon
- 7. La Fleur de Vie
- 8. Le jeu de dés
- 9. L'arbre des trois Mondes
- 10. La Divine Matrice
- 11. La Numérologie
- 12. La GéoNumérologie