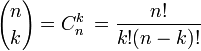Le triangle de Pascal
Le triangle de Pascal révèle des connexions inattendues entre des thèmes aussi variés que les nombres figurés, le calcul combinatoire,
le jeu aux dés, l’hyperdimension, le Tarot de Marseille, la Fleur de Vie, les puissances de 2.
Il permet notamment de lever le voile sur les nombres mystérieux 153 et 666.
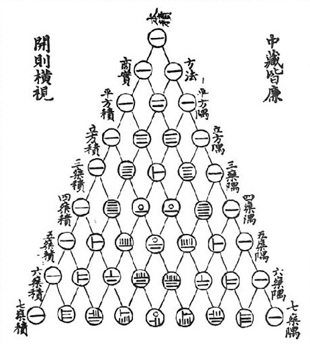
Principes de l'art combinatoire
ou les coefficients binomiaux
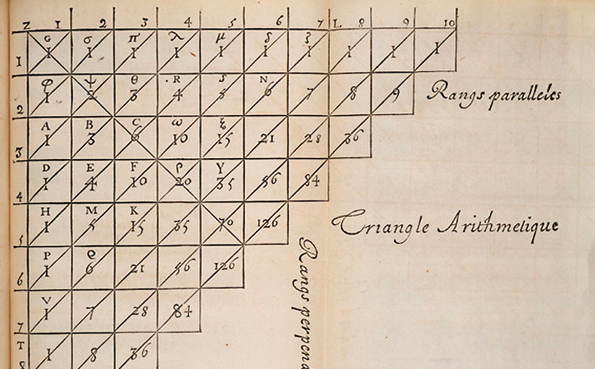
Le triangle de Pascal tient son nom au fait que Blaise Pascal soit l’auteur d’un Traité à son sujet, le Traité du Triangle Arithmétique (1654). Cependant il était déjà connu des mathématiciens arabes du Xe siècle et on retrouve sa trace en Chine au XIe siècle. Il apparait dans le Miroir de jade des quatre éléments de Zhu Shijie en 1303 (visuel ci-contre).
Le triangle de Pascal permet la visualisation des coefficients binomiaux sous la forme d’un triangle.
De quoi s’agit-il ? Tout simplement de définir le nombre de groupes composés de p éléments que l’on peut former dans un ensemble total de n éléments. Il s’agit de combinaisons et non d’arrangements, l’ordre n’intervient pas (AB = BA).
- Symbolisme : Tri-unité, Tarot, jeu de dés, hyperdimension, ...
- Archétype : addition théosophique, puissances de 2
- Géométrie : les nombres triangulaires
- Esotérisme : nombres bibliques, le nombre 2016
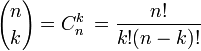 Formule de calcul des coefficients binomiaux ou plus simplement du nombre de groupe de k éléments que vous pouvez former dans un ensemble de n éléments.
Formule de calcul des coefficients binomiaux ou plus simplement du nombre de groupe de k éléments que vous pouvez former dans un ensemble de n éléments.
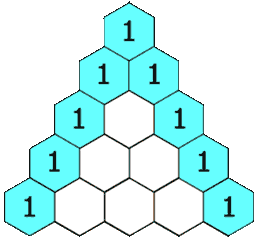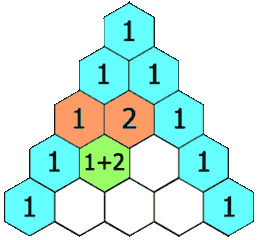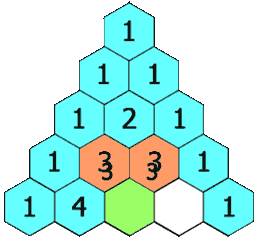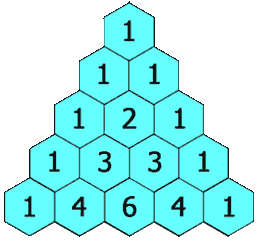
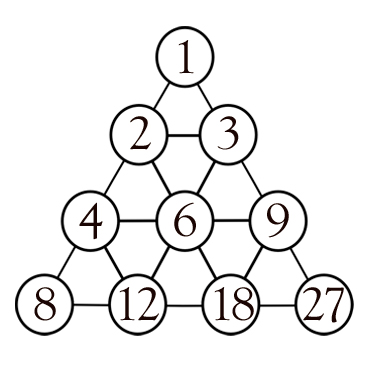
Construction du triangle La Tri-unité originelle
La construction du triangle consiste à placer une tri-unité au sommet d’un triangle. Les extrémités des lignes sont toujours constituées de 1. Les autres nombres sont la somme des deux nombres directement au-dessus. Ex : 2 = 1 + 1; 3 = 1 + 2; etc
Initiation au calcul combinatoire
Le dénombrement des paires
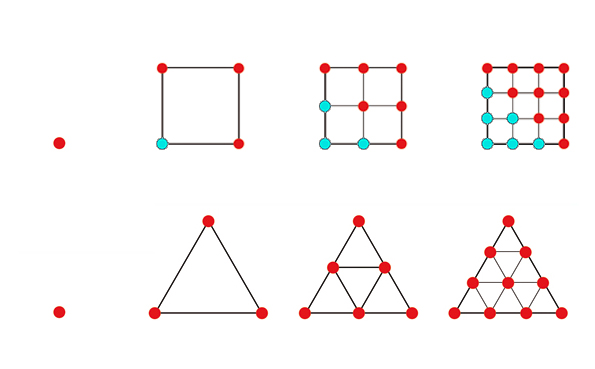
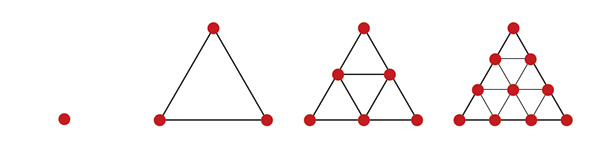
Les nombres triangulaires marquent la première étape de la logique combinatoire en commençant par le dénombrement des relations deux à deux, entre deux points, deux mots ou deux personnes pris dans un groupe de n éléments.
Entre deux personnes il n’existe qu’une possibilité de former un “couple”, d’établir un lien.
Parmi trois personnes, il existe 3 cas de figures : ab, ac et bc.
Dans un groupe de quatre personnes, le nombre de combinaisons s’élève à 6 :
ab, ac, ad, bc, bd et cd.
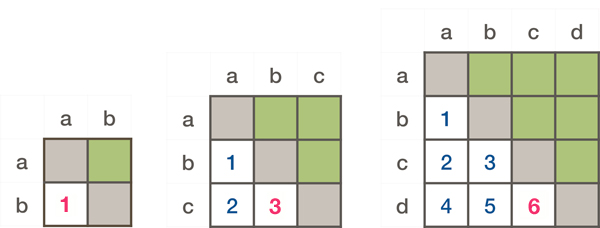
Dans le calcul des combinaisons, l’ordre n’intervient pas. Les cases vertes représentent les doublons : ab = ba.
Le nombre 1 représente la ligne tracé entre deux points (a et b); le nombre 3 représente le nombre de lignes qu’il est possible de tracer dans un ensemble de trois éléments (ou triangle abc);
le nombre 6, le nombre de lignes que l'on peut établir dans un ensemble de 4 éléments (ou carré abcd); etc
On peut écrire aussi : le nombre 1 représente la ligne tracé entre deux points (a et b); le nombre 3 représente le nombre de lignes qu’il est possible de tracer dans un ensemble de trois éléments (ou triangle abc);
le nombre 6, le nombre de lignes que l'on peut établir dans un ensemble de 4 éléments (ou carré abcd); etc
Triangle de Pascal et hyperdimension
Évolution du triangle dans les dimensions supérieures
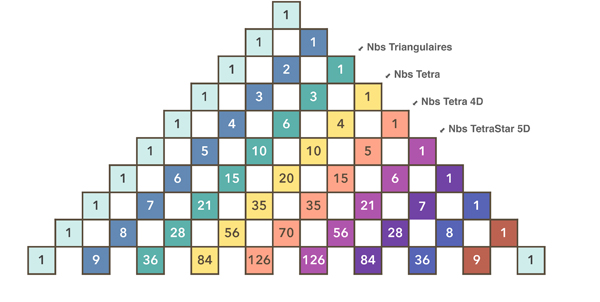
Dans le schéma ci-contre sont visualisées les 10 premières lignes du triangle. Chaque diagonale correspond à une famille de nombres figurés :
- La deuxième diagonale correspond aux nombres entiers, qui additionnés donnent
- les nombres triangulaires 2D, qui additionnés donnent ...
- les nombres tétraédriques 3D , qui additionnés donnent ...
- les nombres hypertétraédriques 4D , qui additionnés donnent ...
- les nombres étoilés tétraédriques 5D , qui additionnés donnent ... etc
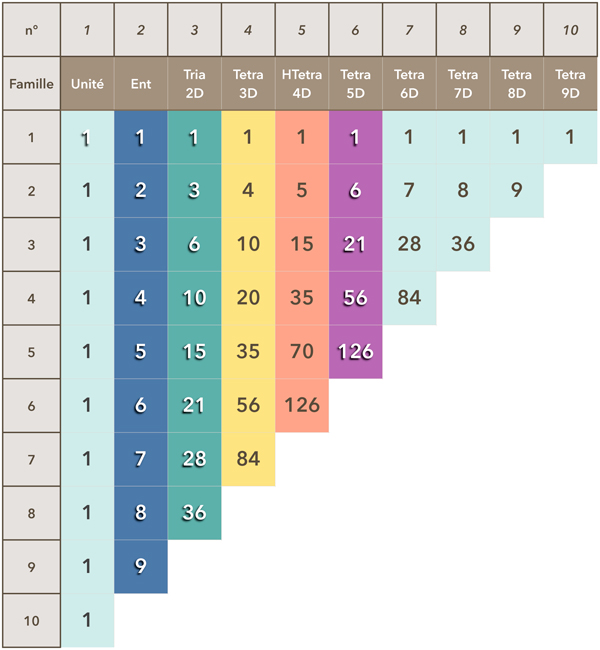
Le triangle de Pascal
Disposition matricielle
Nombres tétraédriques 3D, 4D et 5D
D
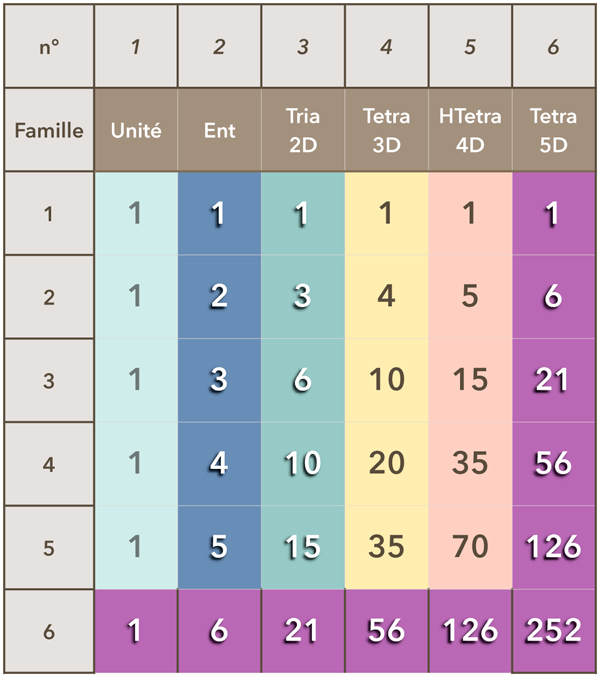
Dans cette disposition, chaque nombre du triangle correspond à l’addition des nombres situés directement à gauche et au dessus de lui. Exemple : le nombre 20 Tetra 3D (ligne 4 - colonne 4) s’obtient par l’addition de 10 + 10; le nombre 28 Tria 2D, par 21 + 7; etc
Les données du triangle sont symétriques de part et d’autre de la diagonale qui part du coin en haut à gauche et est formée des nombres 1, 2, 6, 20, 70, etc
Les nombres tétraédriques représentent le nombre de trinômes ou groupe de 3 éléments (ou triangle) qu’il est possible de former dans un ensemble de n éléments. Dans un groupe de 3, on ne peut former qu’un triangle, 4 dans un groupe de 4 (ou carré); 10 dans un groupe de 5 (ou pentagramme) et enfin 20 dans un groupe de 6 (ou hexagramme).
Les nombres hypertétraédriques de 4D représentent le nombre de groupes de 4 éléments (ou tétraèdre) qu’il est possible de former dans un ensemble de n éléments. Dans un groupe de 4, on ne peut créer qu'un seul tétraèdre, 5 dans un groupe de 5; 15 dans un groupe de 6 et 35 dans un groupe de 7.
Les nombres TetraStar de 5D représentent le nombre de groupes de 5 éléments (ou hypertétraèdre) qu’il est possible de former dans un ensemble de n éléments. Dans un groupe de 5, on ne peut créer qu'un seul hypertétraèdre, 6 dans un groupe de 6; 21 dans un groupe de 7 et 56 dans un groupe de 8.
Le nombre 1
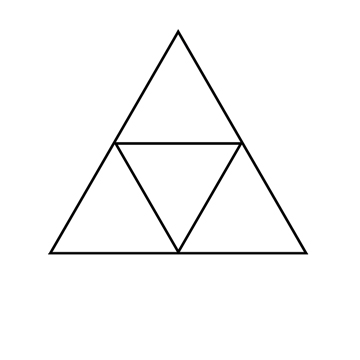
Le nombre 3
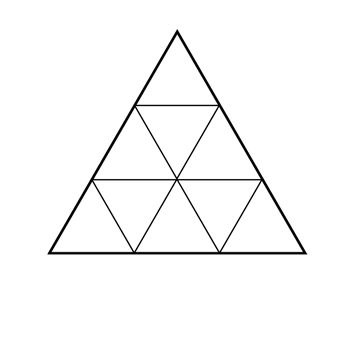
Le nombre 6
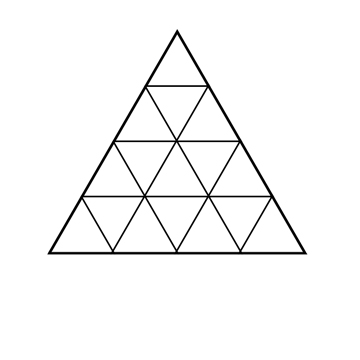
Le nombre 10
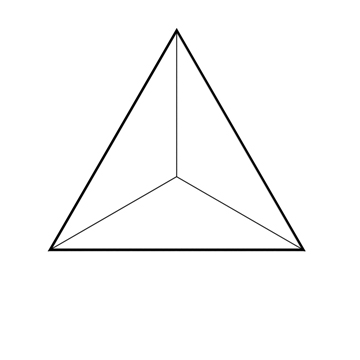
Le nombre 1
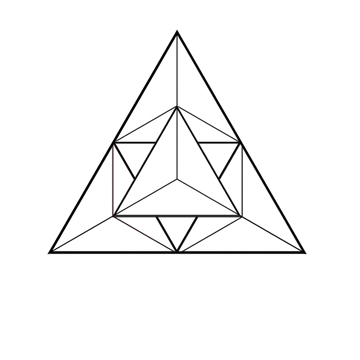
Le nombre 4
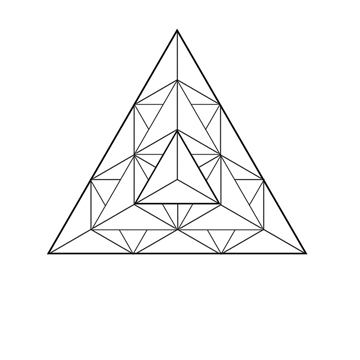
Le nombre 10
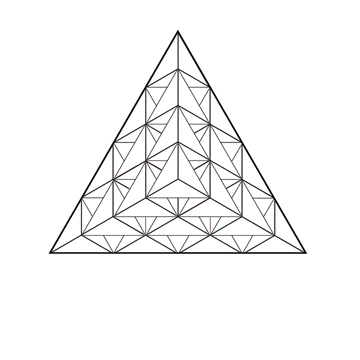
Le nombre 20

Le nombre 1
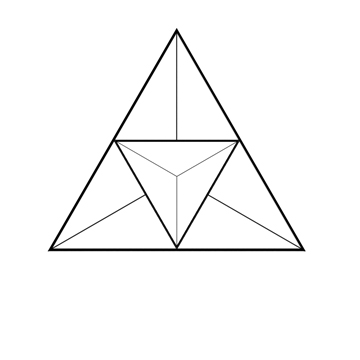
Le nombre 5
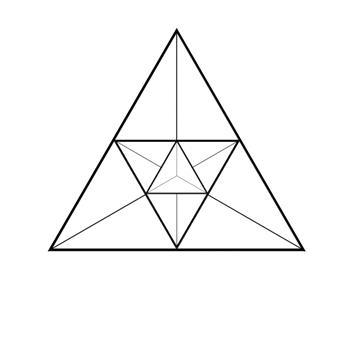
Le nombre 15
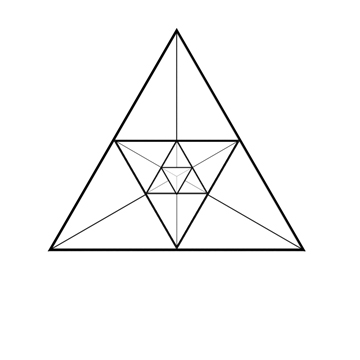
Le nombre 35

Le nombre 1
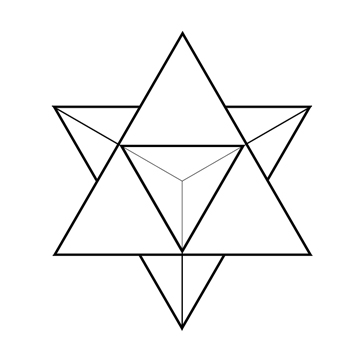
Le nombre 6
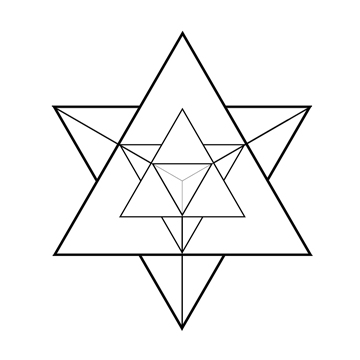
Le nombre 21
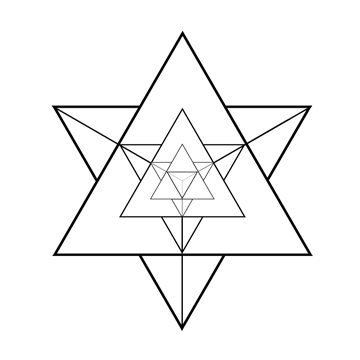
Le nombre 56
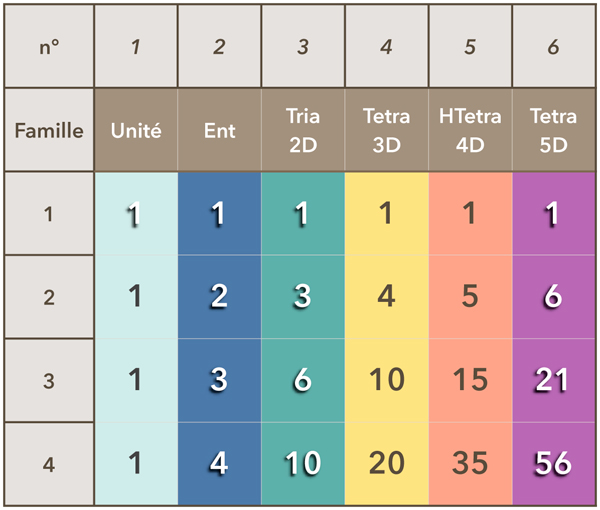
Zoom sur
L'hyperdimension du triangle
Chaque nombre de ce tableau s'obtient en additionnant le nombre à gauche et le nombre au dessus du nombre recherché. Ex : le nombre 21 s'obtient par l'addition des nombres 6 et 15.
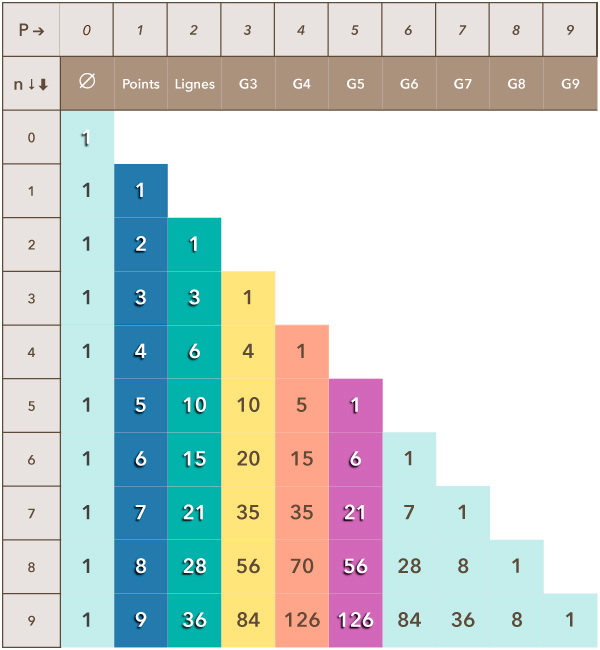
Le triangle de Pascal et l'art combinatoire
Principe de géométrie combinatoire
Dans le tableau ci-contre la première colonne correspond à l'ensemble étudié (composé de n éléments). La première ligne indique le groupe p étudié. Le deuxième ligne indique le nom du groupe étudié (G3 : groupe de 3 éléments). La première colonne correspond à "aucune combinaison".
Les colonnes : le type d"élément présent dans le système
Col n°1 : les nombres entiers correspondent au nombre de points présents dans un ensemble composé de n éléments : 1 point dans un point, 2 points dans une ligne, 3 points dans un triangles; etc
Col n°2 : les nombres triangulaires correspondent au nombre de lignes présentes dans un ensemble composé de n éléments : 1 ligne dans 1 ligne, 3 lignes dans un triangle, 6 lignes dans un carré; etc
Col n°3 : les nombres tétraédriques correspondent au nombre de triangles qu'il est possible de tracer dans un ensemble composé de n éléments : 1 triangle dans 1 triangle (G3), 4 triangle dans un tétraèdre (G4) ou un carré (G4), 10 triangle dans un pentagramme (G5) ou un hypertétraèdre (G5); etc
etc
Les lignes : le nombre total d'éléments du système
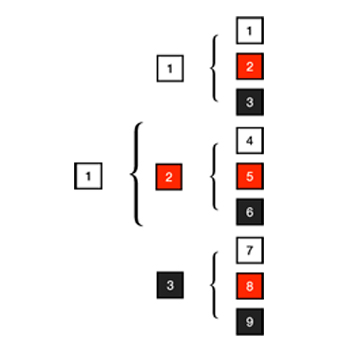
Ligne n°1 : dans un groupe constitué d’un seul élément, nous avons 2 possibilités : 1 point (col 1) ou rien : ∅ (colonne 0).
Ligne n°2 : Dans un groupe de 2 éléments, nous avons 4 possibilités : 2 points (col 1), qui une fois liés, forment 1 ligne (col 2) ou rien : ∅ (col 0).
Ligne n°3 : Dans un groupe de 3 éléments, nous avons 8 possibilités : 3 points (col 1), 3 lignes (col 2), 1 triangle (col 3) ou rien : ∅ (col 0).
Etc
Triangle de Pascal et jeu de dés
Nombres 1, 6, 21, 56
Les nombres tétraédriques de 5D : 1, 6, 21, 56, etc (colonne 6 dans le tableau ci-contre) correspondent aux nombres de combinaisons uniques avec un jeu comportant n dés.
Avec un seul dé il existe 6 possibilités différentes : ⚀⚁⚂⚃⚄⚅
Avec deux dés il existe 36 possibilités différentes : ⚀⚁⚂⚃⚄⚅ X ⚀⚁⚂⚃⚄⚅
Avec trois dés il existe 216 possibilités différentes : ⚀⚁⚂⚃⚄⚅ X ⚀⚁⚂⚃⚄⚅ X ⚀⚁⚂⚃⚄⚅
Après avoir retiré les doublons :
- Ex : ⚀⚁ et ⚁⚀ (jeu à 2 dés);
- Ex : ⚀⚁⚂, ⚀⚂⚁, ⚁⚀⚂, ⚁⚂⚀,⚂⚀⚁, ⚂⚁⚀ (jeu à 3 dés).
le nombres de combinaisons uniques est de :
- 6 pour 1 dés et 6 pour 1 dés;
- 21 pour 2 dés et 21 pour 2 dés;
- 56 pour 3 dés et 56 pour 3 dés;
- etc.
Vous remarquerez que les nombres 21 & 56 sont également le nombre d’Arcanes Majeurs et d’Arcanes Mineurs du Tarot de Marseille.
Le triangle de Pascal et les puissances de 2
Le Tout et ses parties
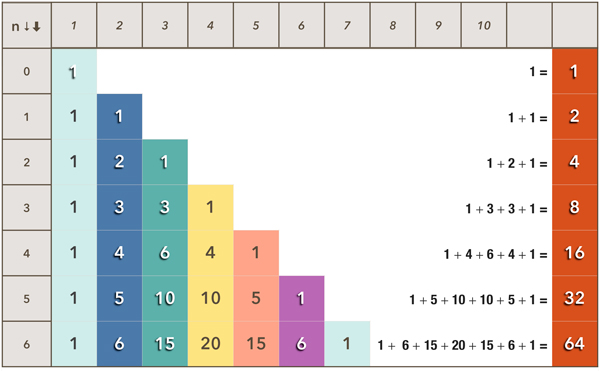
Si on additionne les nombres de chaque ligne, soit l’ensemble des combinaisons possibles dans un ensemble à n éléments, on s’aperçoit que la progression forme la série des Puissances de 2 : 1, 2, 4, 8, 16, 32, 64, 128, 256, etc.
Cette suite, dont les quatre premiers termes font partie de la matrice archétype (nombres 1, 2, 4 et 8) ainsi que de l'Âme du Monde, est reliée aux phénomènes ondulatoires, caractéristiques de l’homme.
La progression des puissances de 2 correspond en tout point aux ramifications de l’arbre généalogique de même qu'au processus de division cellulaire.
Les nombres 153 et 666
Dans les profondeurs du triangle
Les nombres 153 et 666 sont respectivement les 17eme et 36eme nombres triangulaires. Or d'après le principe combinatoire, nous savons que les nombres 153 et 666 représentent également le nombre de couples, lignes ou relations binaires qu'il est possible de former dans un ensemble de :
- 18 éléments pour le nombre 153
- 37 éléments pour le nombre 666
« Simon Pierre monta dans la barque, et tira à terre le filet plein de cent cinquante-trois grands poissons; et quoiqu'il y en eût tant, le filet ne se rompit point . »
Jean 21:11
Le mot filet du latin rete, signifie aussi maillage, réseau. Il a donné le terme de réticulation pour définir les structures en réseau.
Afin de comprendre l’énigme des 153 poissons ou du nombre de la Bête, 666, ce n’est pas au rang (17 et 36) qu’il faut s’intéresser mais bien au nombre qui génère les “connexions divines”, en l’occurrence, les nombres 18 et 37.
« C'est ici la sagesse. Que celui qui a de l'intelligence calcule le nombre de la bête. Car c'est un nombre d'homme, et son nombre est six cent soixante-six ».
Apocalypse de Jean 18:13
Par exemple dans un ensemble de 4 personnes disposées en carré, on peut former 6 couples ou tracer 6 lignes. Le nombre 6 est le 3ème nombre triangulaire (Tableau ci-contre). Ainsi le nombre 153, 17ème nombre triangulaire, correspond au nombre de lignes que l’on peut établir dans un ensemble de 18 éléments et le nombre 666, 36ème nombre triangulaire, au nombre de connexions binaires, ou lignes, que l’on peut tracer entre deux éléments pris parmi un ensemble de 37.
Vous avez aimé cet article ?
Alors partagez-le avec vos amis en cliquant sur les boutons ci-dessous :
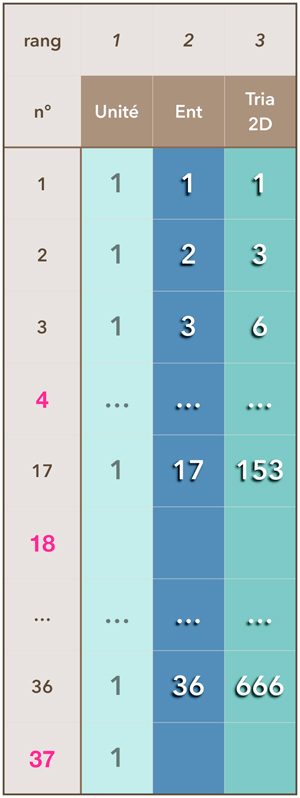
Les nombres 153 et 666
17eme et 36eme nombre triangulaire
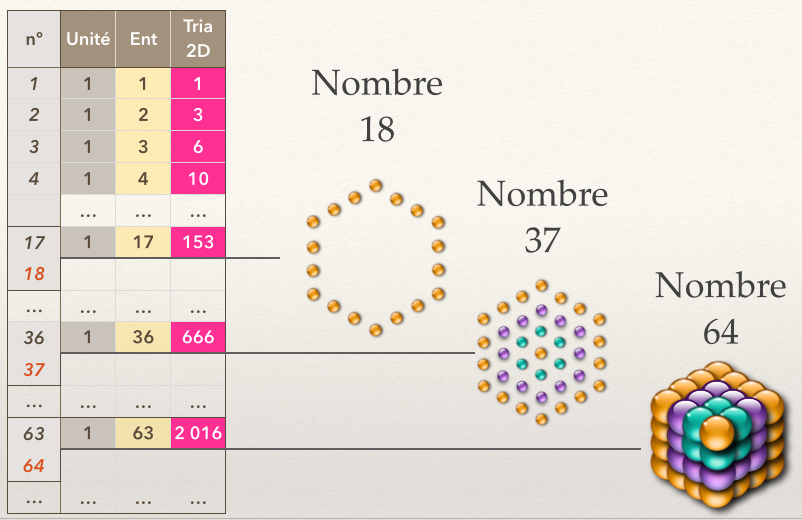
Les nombres triangulaires 153, 666 et 2016 Dela 2D à la 3D
Le nombre 2016 correspond au nombre de couples qu'il est possible de former parmi un ensemble de 64 éléments.
Afin de comprendre l’énigme des 153 poissons ou du nombre de la Bête, le fameux 666,
ce n’est pas au rang (17 et 36) qu’il faut s’intéresser mais bien au nombre qui génère les “connexions divines”, en l’occurrence, les nombres 18 et 37.
Ainsi le nombre 153, 17eme nombre triangulaire, correspond au nombre de lignes que l’on peut établir dans un ensemble de 18 éléments
et le nombre 666, 36ème nombre triangulaire, au nombre de connexions binaires, ou lignes, que l’on peut tracer entre deux éléments pris parmi un ensemble de 37 éléments.
« C'est ici la sagesse. Que celui qui a de l'intelligence calcule le nombre de la bête. Car c'est un nombre d'homme, et son nombre est six cent soixante-six ».
Apocalypse de Jean 18:13
Il existe donc bien une manière spécifique de compter dans la Bible, sinon pourquoi serait-il écrit « calcule le nombre ».
La Bible, que ce soit à travers l’Ancien testament rédigé en hébreu ou le Nouveau, rédigé en grec, est un document écrit avec des nombres.
Ces deux civilisations ne disposant pas de signes particuliers pour les désigner employaient les lettres de l’alphabet pour figurer les nombres.
Combinatoire et hyper dimension du triangle

Les 3 points-clefs
NNombres et Structure:
Le triangle de Pascal est une représentation arithmétique qui révèle des connexions inattendues entre les nombres figurés, le calcul combinatoire, et des concepts ésotériques. Il permet de visualiser les coefficients binomiaux sous la forme d’un triangle, où chaque nombre est la somme des deux nombres directement au-dessus de lui. Par exemple, 2 = 1 + 1; 3 = 1 + 2. Les nombres figurés comme les nombres triangulaires, tétraédriques, et hypertétraédriques sont illustrés dans ce triangle, montrant comment les dimensions évoluent.
FFormes et Géométrie:
Le triangle de Pascal permet la visualisation des combinaisons binomiales, ce qui est essentiel pour le calcul combinatoire. Il montre comment on peut former des groupes de p éléments parmi un ensemble de n éléments. Les formes géométriques issues de ce triangle, telles que les nombres triangulaires et tétraédriques, illustrent des concepts allant des jeux de dés à la géométrie hyperdimensionnelle. La progression des puissances de 2 dans chaque ligne du triangle reflète des structures géométriques fractales, essentielles pour comprendre des phénomènes naturels et ésotériques.
IIdées et Symbolisme:
Le triangle de Pascal est profondément lié à des thèmes symboliques et ésotériques. Par exemple, les nombres 153 et 666, respectivement 17ème et 36ème nombres triangulaires, ont des significations bibliques et ésotériques profondes. Le nombre 153 est associé à la pêche miraculeuse dans l'Évangile de Jean, tandis que le nombre 666 est connu comme le nombre de la Bête dans l'Apocalypse de Jean. Ces nombres illustrent les "connexions divines" et montrent comment des concepts spirituels et mathématiques s’entrelacent. Le triangle de Pascal, en intégrant des puissances de 2 et en reliant des idées combinatoires à des symboles mystiques, dévoile une compréhension profonde de l'univers et de ses mystères cachés.