Les nombres polygonaux s'obtiennent en additionnant les suites arithmétiques
à croissance linéaire.
Chaque élément d'une telle suite permet de déduire le suivant en lui ajoutant une constante appelée raison. Sn+1 = Sn + r
Les nombres entiers forment une suite infinie de raison 1 : 1, 2, 3, 4, 5, 6, etc puisque chaque terme s"obtient en ajoutant le nombre 1 au précédent.
Les nombres impairs forment une suite infinie de raison 2 : 1, 3, 5, 7, 9, etc puisque chaque terme s"obtient en ajoutant le nombre 2 au précédent.
La suite de raison 3 s'obtiendra donc en ajoutant successivement le nombre 3 : 1, 4, 7, 10, etc.
Les nombres triangulaires s'obtiennent en additionnant les nombres de la suite de raison 1 :
1 + 2 : 3;
1 + 2 + 3 = 6;
1 + 2 + 3 + 4 = 10
etc
Les nombres carrés s'obtiennent en additionnant les nombres de la suite de raison 2 :
1 + 3 : 4;
1 + 3 + 5 = 9;
1 + 3 + 5 + 7 = 16
etc
Les nombres pentagonaux s'obtiennent en additionnant les nombres de la suite de raison 3 :
1 + 4 = 5
1 + 4 + 7 = 12
1 + 4 + 7 + 10 = 22
etc
Vous avez aimé cet article ?
Alors partagez-le avec vos amis en cliquant sur les boutons ci-dessous :
Décomposition du nombre.
Les quatre familles de nombres figurés ci-contre ont toutes leur axe de symétrie au sommet de la figure et non au centre. Arthuro Reghini dit de ces familles dans Les Nombres Sacrés, qu’elles ne sont pas isotropiques, à savoir « que les propriétés ne sont plus identiques quelque soit la direction d’observation. »
Leur étude relève plus d’une approche polygonale que d’une logique arithmétique. Ainsi en est-il du pentagone, de l’hexagone et de l’octogone.
Seules nous intéressent les familles de nombres figurés bénéficiant d’un caractère isotropique dans leur progression, à travers un axe de symétrie situé au centre de la figure.
Ainsi il est possible de comparer toutes les figures selon le même référentiel spatial, la même grille de construction. Seule cette condition permet de visualiser correctement la genèse des nombres dans le temps et leurs interactions dans l’espace.
« La géométrie était avant la création des choses, éternelle comme le Divin Esprit; bien plus, elle est Dieu, et c’est elle qui lui a donné les clefs pour la création du monde. »
Johannes Kepler ~ Harmonices Mundi 1619
Origine du calcul.
La décomposition arithmétique du nombre permet de visualiser le nombre en fonction du nombre d'unités qui le composent :
La géométrie sacrée.
La construction des nombres figurés sélectionnés dans la section suivante disposent tous d'un axe de symétrie central et peuvent tous être visualisés soit à l'aide de point soit à l'aide de l'une des trois figures mères. Dans le visuel ci-contre, les nombres triangulaires sont représentés :
De l'intérêt d'une vision isotropique.
SSuites Arithmétiques
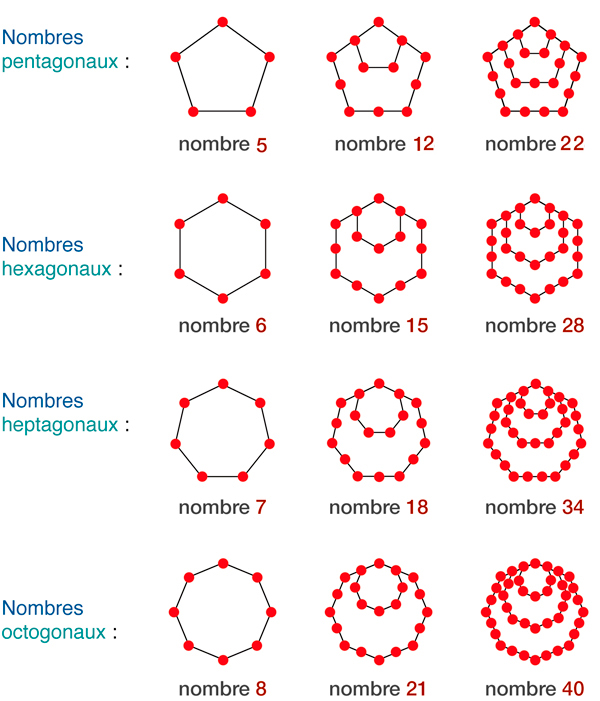
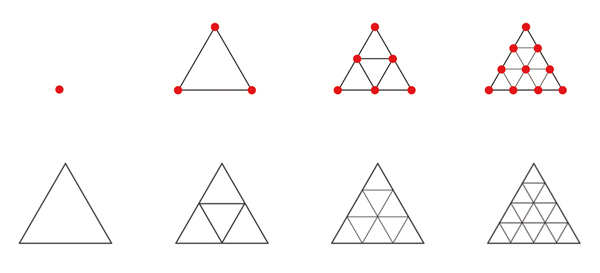
Les nombres polygonaux se forment par addition de suites arithmétiques à croissance linéaire, où chaque élément est obtenu en ajoutant une constante, appelée raison, au précédent. Par exemple, les nombres entiers forment une suite de raison 1 : 1, 2, 3, 4, 5, etc. Les nombres impairs forment une suite de raison 2 : 1, 3, 5, 7, 9, etc. Les suites de raison 3 suivent la progression 1, 4, 7, 10, etc. Les nombres triangulaires s'obtiennent en additionnant les termes de la suite de raison 1 (1 + 2 = 3, 1 + 2 + 3 = 6, etc.). Les nombres carrés s'obtiennent par la suite de raison 2 (1 + 3 = 4, 1 + 3 + 5 = 9, etc.), tandis que les nombres pentagonaux utilisent la suite de raison 3 (1 + 4 = 5, 1 + 4 + 7 = 12, etc.). Cette structure arithmétique révèle les relations entre les figures géométriques et les nombres, illustrant une progression harmonieuse et régulière.
ILa Nécessité des Familles de Nombres Isotropiques
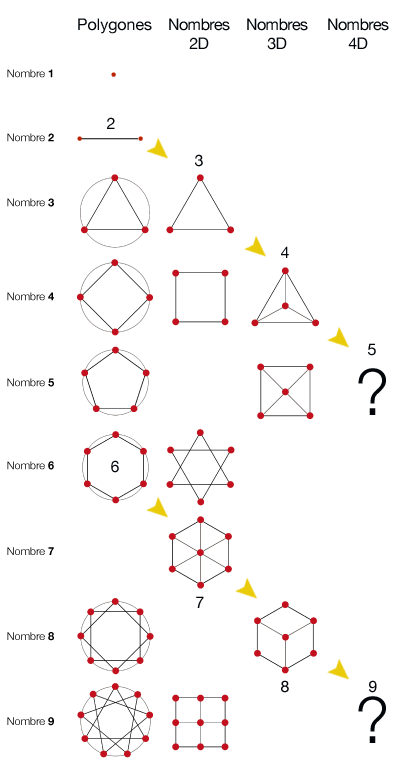
Il est crucial d'opérer avec des familles de nombres dont l'axe de symétrie se trouve au centre, car elles possèdent des propriétés isotropiques. Ces propriétés permettent de traiter tous les nombres sur des grilles centrées, assurant une progression uniforme dans toutes les directions. En utilisant des grilles centrées, nous pouvons comparer et analyser les nombres selon un référentiel spatial cohérent. Cette méthode permet non seulement de visualiser les nombres dans des dimensions plus élevées, mais aussi de comprendre leurs interactions complexes.
VVisualisation des Nombres en 4D et Plus
En procédant par itération, il devient possible de visualiser les nombres dans des dimensions supérieures comme la 4D et au-delà. Chaque itération ajoute une nouvelle dimension de complexité, permettant de voir comment les figures et les nombres se projettent et interagissent dans des dimensions supérieures. Cette technique offre une perspective multidimensionnelle, aidant à comprendre les propriétés et les relations des nombres et des figures géométriques dans des contextes plus avancés et abstraits.
2007 ~ 2024 © symbolinks.com ALL Rights Reserved.
