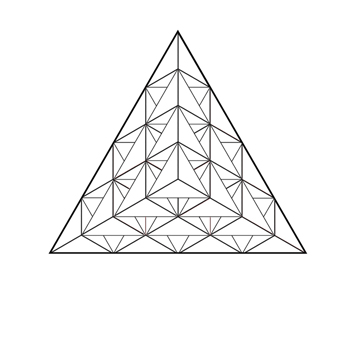
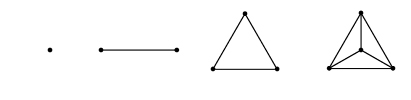Construction des nombres tétraédriques de 3D
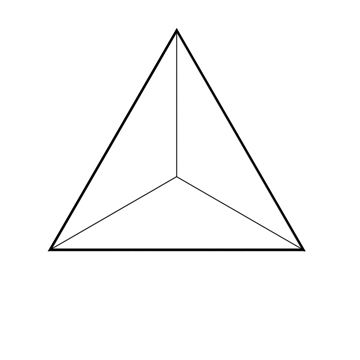
Le centre & le sommet
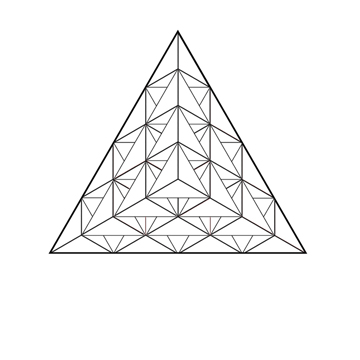
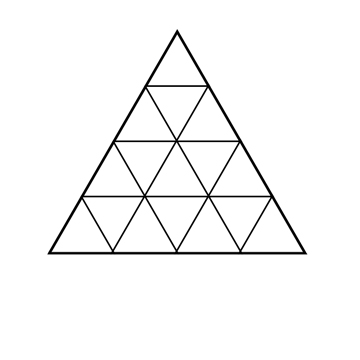
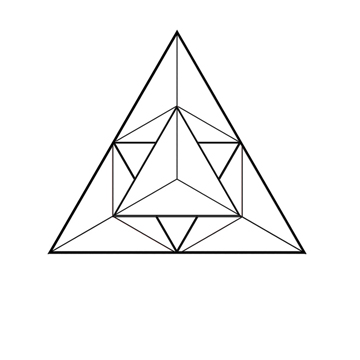
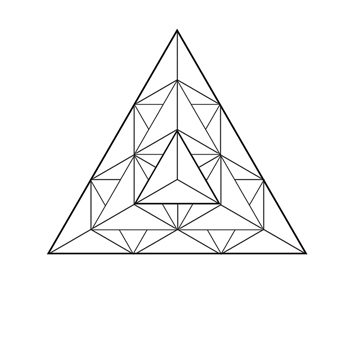
Les nombres tétraedriques représentent la première famille de nombres figurés en volume (epace 3D). Pour représenter les nombres en volume, il est préférable d'utiliser la figure mère comme unité de mesure à la place du point (intersections des lignes sur les illustrations ci-contre).
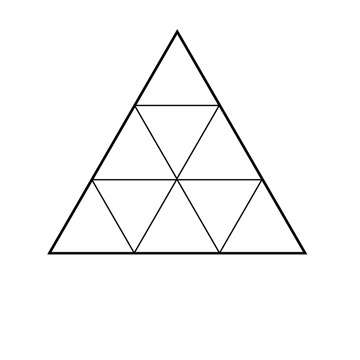
Les nombres tétraédriques s'obtiennent par addition des nombres triangulaires :
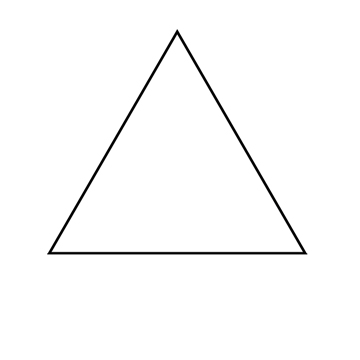
- 1 = 1
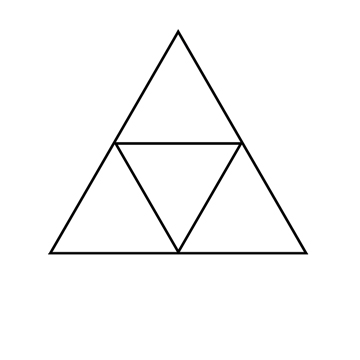
- 4 = 1 + 3
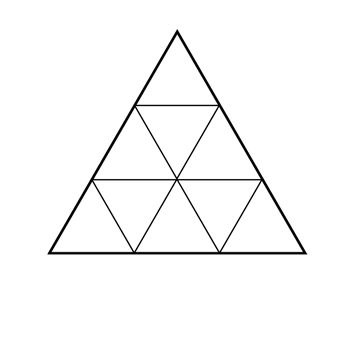
- 10 = 1 + 3 + 6
- 20 = 1 + 3 + 6 + 10
- etc
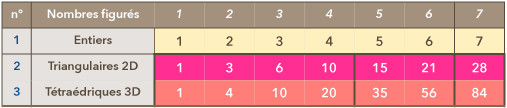
Le nombre 10 est à la fois le quatrième nombre triangulaire et le troisième nombre tétraédrique.
De même que le triangle est la première figure fermée de 2D, le tétraèdre est le premier volume ou solide de 3D.
De même qu’il faut :
- 2 points pour construire une ligne,
- 3 lignes pour un triangle,
- 4 triangles pour un tétraèdre,
- il faudra donc utiliser 5 tétraèdres pour passer à la dimension supérieure.